
If the energies associated with 1st, 2nd, 3rd., nth orbits in the hydrogen atom be E 1, E 2, E 3 … E n, according to the energy equation of the Bohr model,Į 1 ㄑ E 2 ㄑ E 3 ㄑ…ㄑE n Energy equation in Bohr model Because with increasing n, r also increases and orbit makes less stable. Where E 1 = energy of the first orbit of the hydrogen atom in the Bohr model.Īs the principal quantum number increases the energy becomes less negative and hence the Bohr system becomes less stable. Putting the values of π, m, e, and h in the above expression of E, we get the numerical values of E 1. The energy of an electron moving in one particular energy level of the hydrogen atom in the Bohr models can be calculated by the total energy or the sum of the kinetic energy and the potential energy of an electron. When we put the values of r = n 2h 2/4π 2me 2 in equation mvr = nh/2π and solve the equation, the velocity in the Bohr electron,įrom the above formula, the velocity of the second orbit will be one-half of the first orbit and one-third of the first orbit, and so on. R n = n 2 × r 1 = n 2 × 0.529 Å Velocity of electron in Bohr modelįrom the principle of quantization to the revolving electron in the hydrogen atom, mvr = nh/2π. The relation between the first Bohr orbit and the nth orbit of the hydrogen atom,

When n = 1, the radius of the first stationary orbit of hydrogen, R = n 2h 2/4π 2me 2 Radius of first orbit of hydrogen atomįrom the above equation, we can easily find out the radius of the permitted energy levels in terms of the quantum number of the hydrogen atom. If we put the value of velocity (v) on mv 2 = e 2/r and rearranged the equation, N = principal quantum number =1,2,3, …, ∞ Radius of hydrogen atomįrom Niels Bohr’s atomic theory, the angular momentum of the electron is an integral multiple of h/2π. The electron may keep on revolving in hydrogen atom energy levels if these two forces act in the opposite direction and must balance each other. Electric force of attraction: Electric force of attraction given from Coulomb’s law between two opposite charges = e 2/r 2Ĭentrifugal force and electric force acted in the opposite direction.Centrifugal force: The centrifugal force = mv 2/r.On the revolving electron in the hydrogen atom, two types of forces act, Let the nucleus has a mass of m′ and the electron has a mass of m, the radius of the circular orbit = r, and the linear velocity of the electron = v. If E 1, E 2, E 3 … denotes the energy levels of 1 (K-shell), 2 (L-shell), 3 (M-shell) …, then the order of energy levels is E 1ㄑE 2ㄑE 3ㄑ… Electron attraction to the nucleus Therefore the energy associated with certain hydrogen energy levels increases with the increase of its distance from the nucleus. The energy levels are designated by numbers 1, 2, 3, … or capital letters, K, L, M, … starting from the nucleus of the atom.
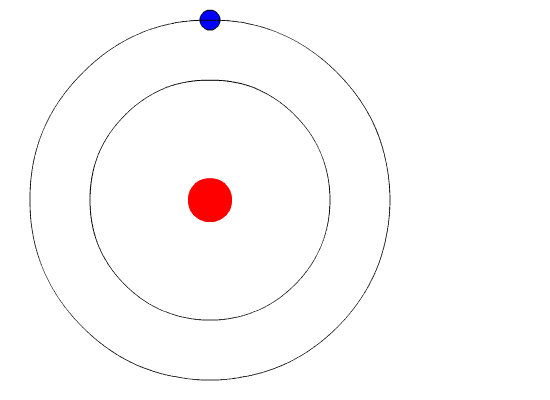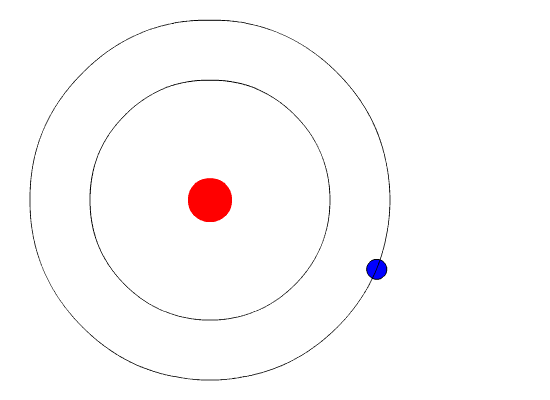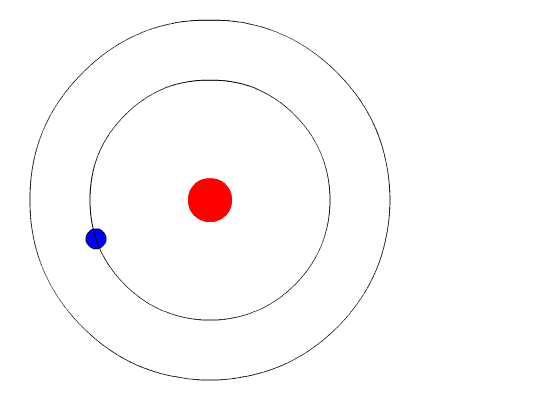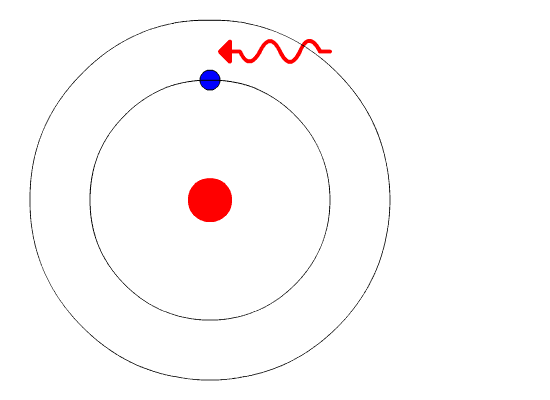
These orbits are called the energy levels of the hydrogen atom.
Hydrogen energy levelsĪn electron stays in a particular orbit where no emission or absorption of energy occurs. This integral multiple is known as the principal quantum energy level of the hydrogen atom.įrom the above postulate, mvr = nh/2π, where m = mass of an electron, v = tangential velocity of an electron, r = radius of Bohr energy levels, and h = 6.627 × 10 −27 erg sec. The angular momentum of an electron moving in an orbit is an integral multiple of h/2π.An electron can jump from one orbit to another higher energy orbit on the absorption of energy but from one orbit to another lower energy orbit with the emission of energy.An electron stays in a particular orbit where no emission or absorption of energy occurs.An atom or hydrogen atom possesses several stable circular orbitals in which an electron can stay.To study chemistry or physics, Bohr’s model of a hydrogen atom is based on several postulates. The Bohr atomic model of the hydrogen atom is similar to that of the solar system of our planet. But the actual electromagnetic spectrum of the hydrogen atom consists of well-defined lines with definite frequencies or wavelengths.įor an explanation of the atomic spectrum, Bohr adopted the Rutherford nuclear model for the hydrogen atom or one electronic system in which an electron revolves around the nucleus. According to classical mechanics, when a charged electron is subjected to acceleration, it emits electromagnetic radiation and hit the nucleus of an atom.Īccording to Rutherford model, the electron loses energy continuously and the observed spectra should be continuous spectra.


 0 kommentar(er)
0 kommentar(er)
